본 게시물은 네이버 부스트코스 주재걸 교수님의 '인공지능을 위한 선형대수' 강의를 듣고 요약하였습니다.
선형 대수 기초
Matrix의 종류
- Square Matrix
- Rectangular Matrix
- Transpose Matrix
- (AB)를 Transpose 하게 되면 B^T, A^T로 순서가 변경됨
- (i, j) component $A(i, j)$
** Vector 도 Matrix의 한 종류로서 생각할 수 있음! **
Linear Equation & Linear System
연립방정식을 선형대수를 이용해 직관적으로 풀이할 수 있음.

이렇게 $Ax = b$ 꼴로 나타낼 수 있는데, 이는 뒤에서 선형 결합 문제 풀이에서 응용할 수 있음.
항등 행렬과 역행렬

- 항등행렬 : Diagonal Entry 가 모두 1이고 나머지는 0인 행렬을 말한다. (어떤 벡터와 곱해도 자기 자신을 만들어 냄)
- 역행렬 : ➡ Det 행렬을 정의할 수 있고, 오직 정사각 행렬(Square Matrix) 에서만 역행렬을 논의할 수 있음!
- $det(A)$가 0이 되는 경우 역행렬이 존재하지 않는다.
- $det(A)$로 판단할 수 있는 것
- Matrix의 역행렬 유무
- 선형 변환에서의 data + 배율 (vector들의 길이를 얼만큼 정하느냐?)
역행렬을 이용해 연립방정식을 푸는 방법은 아래와 같다.
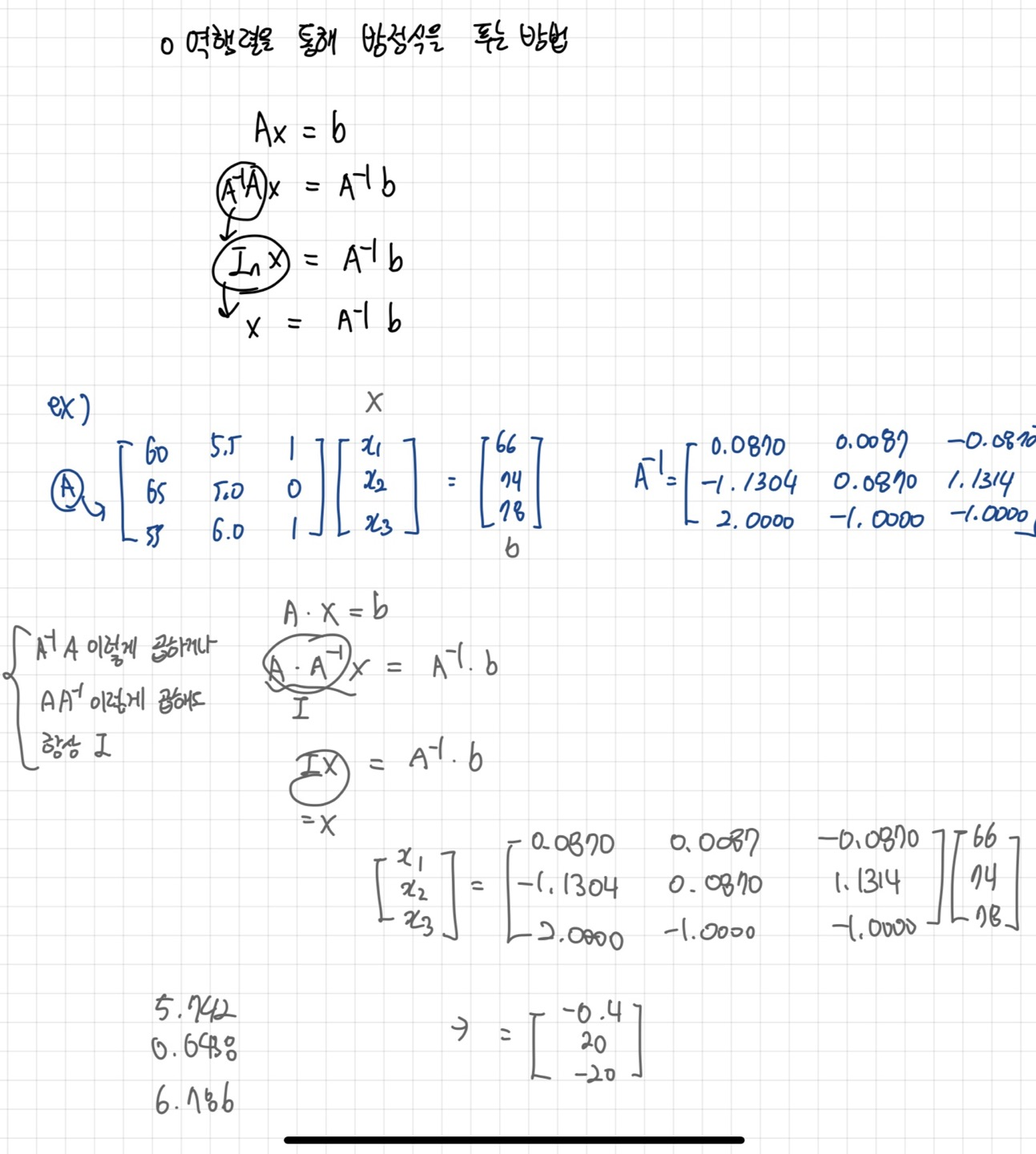
- Inverse Matrix 가 존재하지 않는 경우
- 해가 무수히 많거나
- 해가 하나도 없음
직사각 행렬에서는?
- m<n : feature 개수가 더 많을 때. 해가 무수히 많음 (under-determined)
- m>m : 변수가 적을 때. 해가 존재하지 않음 (over-determined)
→ 따라서 근사적으로 만족하는 경우를 찾아서 풀이한다!
Regularization 적용 (risk minimization)
'딥러닝 기초 > 수학..' 카테고리의 다른 글
| [선형 대수] Linear Transformation (선형 변환) (0) | 2024.03.02 |
|---|---|
| [선형 대수] Basis & Dimension (0) | 2024.03.02 |
| [선형 대수] Linear Combination & Span (0) | 2024.01.18 |

