본 게시물은 네이버 부스트코스 주재걸 교수님의 '인공지능을 위한 선형대수' 강의를 듣고 요약하였습니다.
Linear Combination (선형 결합)
- Matrix equation 을 Vector equation으로 만들기

다음과 같이 행렬방정식을 벡터 방정식으로 변환할 수 있음
Span
- The set of all linear combinations of v1, v2, .... vp
- 선형 결합을 통해 만들 수 있는 벡터 집합을 말한다.

다음과 같은 벡터들이 존재할 때, 벡터의 선형 결합으로 만들어 낼 수 있는 모든 벡터의 존재의 집합을 Span 이라고 한다.
Q. Vector equation으로 봤을 때, $Ax = b$ 의 연립 방정식 해가 존재할 것인가?
- $Ax = b$의 값이 재료벡터 x1, x2, x3로 만들어지는 span에 포함이 되어 있다. → x1, x2, x3의 선형 결합으로 표현할 수 있다.
- $Ax = b$의 값이 재료벡터 x1, x2, x3로 만들어지는 span에 포함되어있지 않다. → 어떤 선형 결합으로도 표현이 불가능하다.
Column vector combination
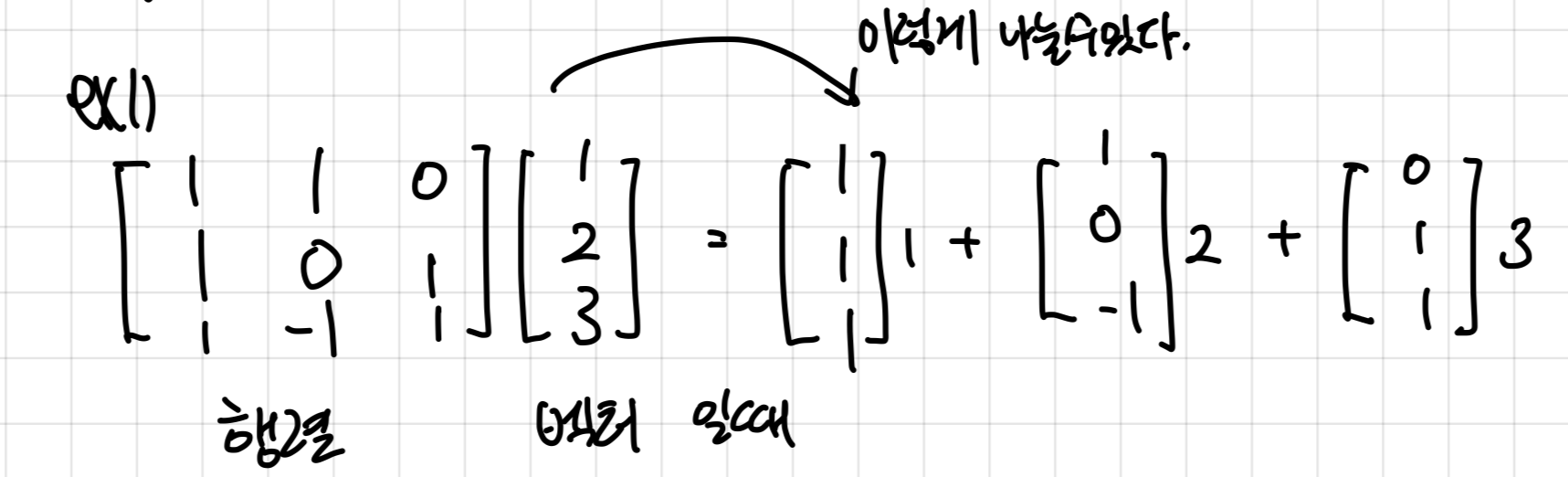

행렬과 벡터가 다음과 같이 존재할 때, 위와 같이 벡터의 coefficient로 나타낼 수 있다.
(방정식의 개수 = coefficient vector의 차원)
Linear Independence
Q. $Ax = b$ 라는 방정식의 해가 존재한다면, 언제 unique(방정식이 하나의 해 만을 갖는가?) 한가?
⇢ 평행사변형이 하나의 평행사변형으로만 그려질 때
- 해가 여러 개 존재 : 선형 의존 (Linearly Dependent)
- Unique 한 해가 존재 : 선형 독립 (Linearly independent)
- &v_j \in span{v_1, v_2, ..., v_(j-1)& 인데, $v_j$ 가 그 전엔 span에 포함되어 있지 않다가 포함되면서 span의 차원을 늘려주게 되는 경우 Linear Independent 하다고 한다.
- 3차원 공간상에서 기존 벡터가 4개일 때, → 항상 기본적으로 '선형 의존(Linear Dependent)'를 만족함.
- '미지수의 개수 > 방정식의 개수'인 경우 해가 무수히 많이 존재한다.
- Vector의 방향성이 같으면 해가 무수히 존재
Homogeneous Equation (동차 방정식)
- $Ax = b$ 식에서 모든 $b$에 대해, $b = 0$이라고 가정
- $x_1 v_1 + x_2 v_2 + ... + x_p v_p = 0$ 으로 표현할 수 있으며, ⇢ 어떠한 vector의 span에도 포함되는 vector가 된다.
- 모든 가중치를 '0'으로 setting 하면서, 언제나 방정식의 최소한의 Solution을 만족한다. ( = trivial solution 이라고 한다. /
하찮은 솔루션이다 해서) - 반대로 non-zero가 존재하는 경우, non-trivial solution 이라고 한다.
예를 들어, $v_3 = 2 v_1 + 3v_2$ 인 경우, $v_3$이 추가되어도 span을 늘려주지 못하기 때문에 Homogenous Linear system이 된다.
Sub Space (span과 유사)
→ 부분집합 + 선형 결합에 닫혀있을 때 (closed under linear combination) 어떤 재료 벡터의 span으로 표현될 수 있는 것을 말함.

예를들어 위와 같은 벡터의 집합이 존재할 때, 먼저 두 개의 벡터를 뽑아서 적당한 선형 결합을 만들고, 만든 선형 결합이 S 안에 존재하게 되는 경우를 '닫혀 있다' 라고 한다.
위 두 조건을 만족할 때, vector들의 부분집합을 subset 이라고 표현하지 않고, sub space 라고 부르게 된다.

'딥러닝 기초 > 수학..' 카테고리의 다른 글
| [선형 대수] Linear Transformation (선형 변환) (0) | 2024.03.02 |
|---|---|
| [선형 대수] Basis & Dimension (0) | 2024.03.02 |
| [선형 대수] 선형 대수 기초 (1) | 2024.01.10 |

